|
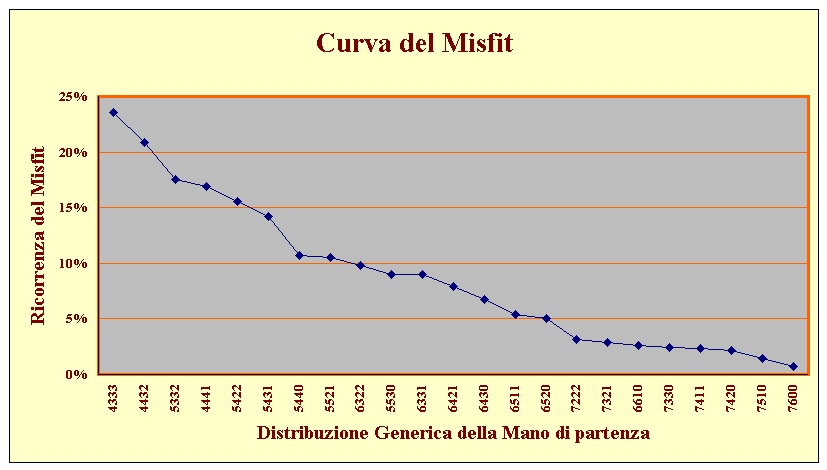
La Curva del Misfit |
Uno degli argomenti meni noti della statistica applicata al bridge, riguarda le probabilità che ha la propria linea di incappare in un completo misfit, partendo con una determinata distribuzione generica di mano.
Quando primi di mano aprite le carte e scoprite di avere una 6.3.2.2, pensate che le vostre probabilità di incappare in una delle due distribuzioni di linea (DL) che prevedono l'assenza di colori almeno ottavi, siano uguali o inferiori a quando invece partite con una 4.3.3.3 ?
Sono certo che pensate che siano inferiori partendo con la 6.3.3.2, tutto sommato basta trovare due sole carte di fit nel colore della lunga per scamparla!
Avete ragione, ma se volete approfondire la questione, scoprirete che non sempre le vostre sensazioni risulteranno allineate con quanto previsto dalle leggi del caso.
Innanzi tutto, ricordiamo che le Leggi del Fit che sono trattate in un altro articolo di questa sezione, ci rivelano che la possibilità di restare privi di un fit almeno ottavo è confinata alla presenza di una delle seguenti due distribuzioni di linea:
| Tabella delle Distribuzioni di Misfit | ||
| DL |
Numero delle Linee |
% |
| 7.7.7.5 | 541.101.550.596.416.000.000 | 5,2 |
| 7.7.6.6 | 270.550.775.298.208.000.000 | 10,5 |
Come potete vedere dalla tabella qui sopra, le DL che sanciscono l'assenza di fit sono solo 2 delle 104 possibili, eppure, da sole, hanno una popolazione che rappresenta un non trascurabile 15,7% dell'intero universo linee.
Se vogliamo però sapere, come esse si suddividono in funzione della distribuzione generica iniziale di una delle due mani che compongono la nostra linea (DM), dobbiamo affrontare un duro lavoro.
Prima di tutto per ognuna delle possibili 23 DM prive di colori ottavi o più, dobbiamo trovare tutte le DM di complemento che portano alla costituzione di una delle due DL di misfit.
Poi utilizzando un procedimento del tutto simile a quello utilizzato per arrivare alla enunciazione delle Leggi del Fit, dobbiamo andare a computare quante combinazioni esistono per ogni possibile incrocio delle due DM che formano una delle nostre due linee di misfit ed, infine, dobbiamo raffrontare i totali parziali così ottenuti, con il totale delle DL che possono formarsi a partire dalla DM considerata.
Il risultato di questo improbo lavoro è rappresentato per le DM più significative nella tabella sottostante.
| DM | p |
| 4333 | 23,60% |
| 4432 | 20,90% |
| 5332 | 17,52% |
| 4441 | 16,93% |
| 5422 | 15,51% |
| 5431 | 14,19% |
| 5440 | 10,73% |
| 5521 | 10,53% |
| 6322 | 9,81% |
| 5530 | 9,00% |
| 6331 | 8,98% |
| 6421 | 7,95% |
| 6430 | 6,79% |
| 6511 | 5,39% |
| 6520 | 5,04% |
| 7222 | 3,16% |
| 7321 | 2,89% |
La colonna p indica la probabilità a priori percentualizzata di incappare in una situazione di completo misfit partendo con la DM di riga.
Come potete vedere è la 4.3.3.3 la DM che più di ogni altra ci porterà in una situazione di completo misfit , seguita a ruota dalla 4.4.3.2 e dalla 5.3.3.2 che, non a caso, tutte insieme, formano il sotto insieme delle mani bilanciate.
Per i costruttori di sistemi licitativi, di seguito viene graficata la curva del misfit dove si può osservare la probabilità a priori di verificarsi di una situazione di completo misfit a partire da una qualsiasi delle 23 DM che possono generarla.
