|
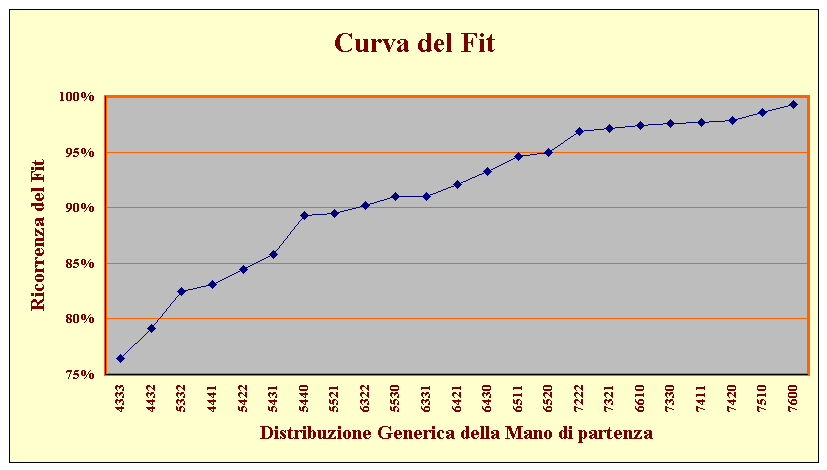
La Curva del Fit |
Con lo stesso metodo usato per calcolare le probabilità a priori di incappare in una situazione di completo misfit partendo con una data DG, possiamo computare quelle di chiudere con la mano del compagno una linea di fit (comprendendo in questa definizione tutte quelle linee che presentano almeno un colore di almeno 8 carte).
|
DG |
LF |
|
4333 |
76,40% |
|
4432 |
79,10% |
|
5332 |
82,48% |
|
4441 |
83,07% |
|
5422 |
84,49% |
|
5431 |
85,81% |
|
5440 |
89,27% |
|
5521 |
89,47% |
|
6322 |
90,19% |
|
5530 |
91,00% |
|
6331 |
91,02% |
|
6421 |
92,05% |
|
6430 |
93,21% |
|
6511 |
94,61% |
|
6520 |
94,96% |
|
7222 |
96,84% |
|
7321 |
97,11% |
|
6610 |
97,42% |
|
7330 |
97,53% |
|
7411 |
97,66% |
|
7420 |
97,82% |
|
7510 |
98,52% |
|
7600 |
99,29% |
Nella tabella è esposta, espressa in percentuale, la probabilità a priori percentualizzata di legare almeno un fit di 8 o più carte, partendo con ognuna delle 23 distribuzioni prive di colori almeno ottavi.
Per una migliore visione d'assieme dei dati esposti in tabella, gli stessi sono stati di seguito graficati.

Nel diagramma è possibile constatare che, con poche eccezioni, è la lunghezza del seme dominante di una mano che influisce sulle probabilità a priori di legare un qualsiasi fit con la mano del compagno.
In particolare, può essere interessante osservare come la tricolore piccola (4.4.4.1), grazie ai suoi tre colori quarti, offra una maggior probabilità a priori di formare un fit almeno Ottavo di quanto non sia possibile sperare di ottenere con la mano unicolore (5.3.3.2), che pure può contare su un colore dominante quinto.
Anche la mano monocolore piccola (6.3.2.2) presenta la stessa particolarità rispetto alla bicolore grande (5.5.3), a dimostrazione che la maggior lunghezza complessiva dei primi tre colori della mano, può arrivare a compensare il fatto di avere il colore dominante più corto di una carta.
Si noti pure come l'aspettativa di legare un fit almeno ottavo partendo con una bicolore piccola, sia mediamente del 5% inferiore a quella che si riscontra partendo con le due monocolori seste, fatto questo, che rende più sicure le tradizionali sottoaperture monocolori anziché le moderne Muiderberg.
Per differenza, potete poi calcolare per conto vostro, quali sono le probabilità a priori di finire in misfit (nessun colore almeno ottavo in linea) partendo con ognuna delle distribuzioni prese in considerazione.