| Le Curve del Fit |
Con lo stesso procedimento con il quale abbiamo tracciato la Curva del Misfit possiamo calcolare la Curva del Fit, cioè la curva che grafica le probabilità a priori del formarsi di una linea con almeno un fit ottavo partendo con una qualsiasi distribuzione generica di mano.
Nella tabella che segue si possono appunto osservare i valori della frequenza percentuale di ricorrenza di un qualsiasi Fit di Linea partendo con una qualsiasi delle possibili 39 distribuzioni generiche.
| DM |
f% |
| 4432 | 17,0473% |
| 5332 | 12,7978% |
| 5431 | 11,0958% |
| 5422 | 8,9383% |
| 4333 | 8,0494% |
| 6322 | 5,0887% |
| 6421 | 4,3284% |
| 6331 | 3,1387% |
| 5521 | 2,8396% |
| 4441 | 2,4866% |
| 7321 | 1,8265% |
| 6430 | 1,2362% |
| 5440 | 1,1099% |
| 5530 | 0,8147% |
| 6511 | 0,6673% |
| 6520 | 0,6183% |
| 7222 | 0,4967% |
| 7411 | 0,3827% |
| 7420 | 0,3538% |
| 7330 | 0,2587% |
| 8221 | 0,1924% |
| 8311 | 0,1165% |
| 8320 | 0,1095% |
| 7510 | 0,1069% |
| 6610 | 0,0705% |
| 8410 | 0,0452% |
| 9211 | 0,0178% |
| 9310 | 0,0100% |
| 9220 | 0,0082% |
| 7600 | 0,0055% |
| 8500 | 0,0031% |
| 10210 | 0,0011% |
| 9400 | 0,0010% |
| 10111 | 0,0004% |
| 10300 | 0,0002% |
| 11110 | 0,0000% |
| 11200 | 0,0000% |
| 12100 | 0,0000% |
| 13000 | 0,0000% |
| Totale | 84,2637% |
Come potete osservare, la DM 4.4.3.2 oltre che essere quella che più di ogni altra forma le linee di misfit è anche quella che più di ogni altra forma le linee di fit.
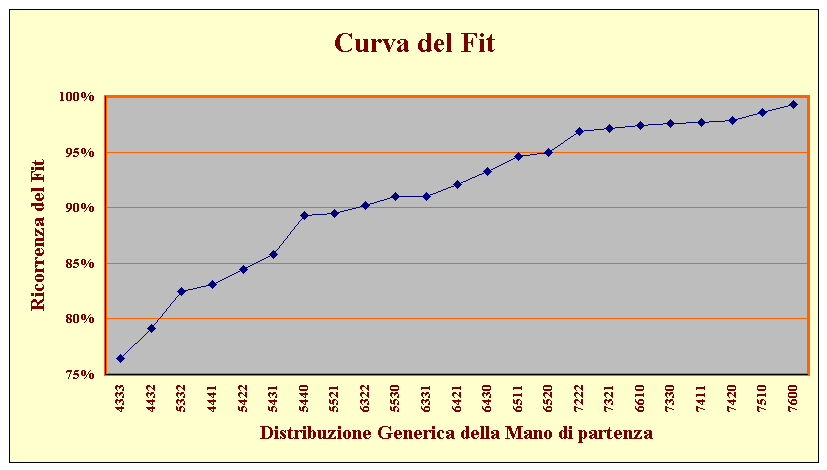
I valori della soprastante tabella sono graficati nel diagramma che segue.

Naturalmente con procedimento analogo possono venire calcolate e graficate tutte le singole curve del fit di linea per ogni possibile lunghezza dello stesso.
Potete prendere visione delle stesse nella altre pagine di questo stesso articolo.